9655. Мистер
Найн и его любовь к манго
Мистер
Найн во время перерывов в середине семестра случайно бродил по вселенной Параллель
и неожиданно наткнулся на манговое дерево. Он любит манго, поэтому решил его
сорвать. Но внезапно появилась фея и дала ему решить сложную задачу. Дерево содержит n узлов.
Заданы также два узла u и v. Фея спрашивает, сколько существует
таких пар узлов в дереве, что кратчайший путь между ними не содержит узла v после узла u (например, u →
a → b → v также не
допускается, где a и b – два разных узла). Если мистер Найн
сможет определить правильное количество пар узлов, то получит все манго. Однако
он не в состоянии это сделать и нуждается в Вашей помощи.
Вход. Первая строка содержит числа n (1 ≤ n ≤ 300005), u и v. Каждая из следующих n – 1 строк содержит два целых
числа x и y означающих присутствие ребра между вершинами x и y (1 ≤ x, y ≤ n).
Выход. Выведите общее количество пар вершин.
|
Пример
входа |
Пример
выхода |
|
3 1 3 1 2 2 3 |
5 |
РЕШЕНИЕ
поиск в
глубину
Анализ алгоритма
Поскольку на вход
дается дерево, то существует единственный путь между u и v. Пусть этот путь имеет вид: u → s → … → t
→ v. Заполним массив parent, чтобы можно было
найти вершины s (следует за u) и t (идет перед v).
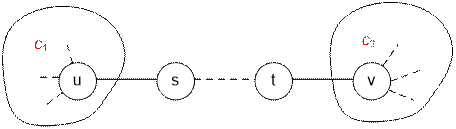
Пусть c1 – количество вершин в
поддереве с корнем u, при условии
удаления ребра (u, s). Пусть c2 – количество вершин в поддереве с корнем v, при условии удаления ребра (t, v).
Количество путей, в которых после u
идет v, равно c1 * c2.
Общее число путей на
графе равно n * (n – 1), где n –
количество вершин. Граф неориентированный, путь из a в b и из b в a считаем разными. Количество искомых пар
вершин равно
n
* (n – 1) – c1 * c2
Пример
Граф из
примера имеет вид:
Существует 5 возможных
пар:
·
(1, 2) : путь 1 → 2
·
(2, 3) : путь 2 → 3
·
(3, 2) : путь 3 → 2
·
(2, 1) : путь 2 → 1
·
(3, 1) : путь
3 → 2 → 1
Найн не
может выбрать пару (1, 3), так как кратчайшим путем между ними будет 1 →
2 → 3 и он не приемлем, так как содержит v = 3 после u = 1, что
не допустимо.
Реализация алгоритма
Объявим список смежности графа g и рабочие массивы.
vector<vector<int>
> g;
vector<int>
used, parent;
Функция dfs реализует поиск в
глубину. Строим массив предков parent.
void dfs(int v)
{
used[v] = 1;
for (int i =
0; i < g[v].size(); i++)
{
int to =
g[v][i];
if
(used[to] == 0)
{
parent[to] = v;
dfs(to);
}
}
}
Функция dfs1 реализует поиск в глубину из вершины v. В переменной c1 подсчитываем количество вершин в поддереве с корнем v, при условии что переход в вершину s запрещен.
void dfs1(int v)
{
used[v] = 1;
c1++;
for (int i =
0; i < g[v].size(); i++)
{
int to =
g[v][i];
if (to
== s) continue;
if
(used[to] == 0) dfs1(to);
}
}
Функция dfs2 реализует поиск в глубину из вершины v. В переменной c2 подсчитываем количество вершин в поддереве с корнем v, при условии что переход в вершину t запрещен.
void dfs2(int v)
{
used[v] = 1;
c2++;
for (int i =
0; i < g[v].size(); i++)
{
int to =
g[v][i];
if (to
== t) continue;
if
(used[to] == 0) dfs2(to);
}
}
Основная часть программы. Читаем входные данные. Строим граф.
scanf("%d %d %d", &n, &start,
&finish);
g.resize(n + 1);
used.resize(n + 1);
parent.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Запускаем поиск в глубину из вершины start.
dfs(start);
Используя массив предков parent, находим вершины s
и t:
start → s → ... → t → finish
t = parent[finish];
s = finish;
while (parent[s] !=
start) s = parent[s];
При помощи поиска в глубину вычисляем значения c1 и c2.
c1 = 0;
used.clear(); used.resize(n + 1);
dfs1(start);
c2 = 0;
used.clear(); used.resize(n + 1);
dfs2(finish);
Выводим ответ.
res = 1LL * n * (n - 1) - c1 * c2;
printf("%lld\n",
res);